树的高度

https://www.geeksforgeeks.org/roots-tree-gives-minimum-height/
Given an undirected graph, which has tree characteristics (any connected graph without simple cycles is a tree.). It is possible to choose any node as root, the task is to find those nodes only which minimize the height of tree.

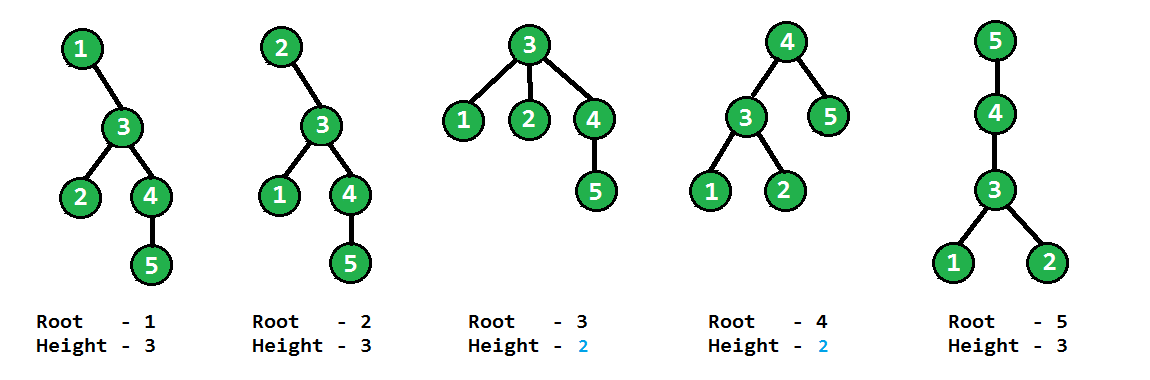
Example:
In below diagram all node are made as root one by one, we can see that when 3 and 4 are root, height of tree is minimum(2) so {3, 4} is our answer.

We can solve this problem by first thinking about the 1-D solution, that is if the longest graph is given, then the node which will minimize the height will be mid node if total node count is odd or mid-two-node if total node count is even. This solution can be reached by the following approach – Start two pointers from both ends of the path and move one step each time until pointers meet or one step away, at the end pointers will be at those nodes which will minimize the height because we have divided the nodes evenly so the height will be minimum.

The same approach can be applied to a general tree also. The center lies in the middle of diameter of this tree. Start pointers from all leaf nodes and move one step inside each time, keep combining pointers which overlap while moving, at the end only one pointer will remain on some vertex or two pointers will remain at one distance away. Those nodes represent the root of the vertex which will minimize the height of the tree.

So we can have only one root or at max two roots for minimum height depending on tree structure as explained above. For the implementation we will not use actual pointers instead we’ll follow BFS like approach, In starting all leaf node are pushed into the queue, then they are removed from the tree, next new leaf node is pushed in the queue, this procedure keeps on going until we have only 1 or 2 node in our tree, which represent the result.

another solution:
https://stackoverflow.com/questions/4020122/finding-center-of-the-tree

run 2 BFS:

Select any vertex v1 on your tree. Run BFS from this vertex. The last vertex (v2) you will proceed will be the furthest vertex from v1. Now run another BFS, this time from vertex v2 and get the last vertex v3.

The path from v2 to v3 is the diameter of the tree and your center lies somewhere on it. More precisely it lies in the middle of it