未看但是可能要看:
- 2.4 分支限界算法中:多项式近似算法,page 35
- 2.4 KT index,page 63
1.1 图的基本概念、类型

1.2 幂律分布、图的测度参数、随机图
2.1 顶点及边的中心性计算

n为全图顶点数目
无向图的度中心性:顶点的度(可以通过除以最大可能值n-1来标准化度数)



2.2 可达性&最短路径
Dijkstra算法:
直到所有顶点都加入集合S

A*算法:
直到所有顶点都加入集合S

其中g(n)的计算:传递计算
2.3 稠密子图搜索
定义和算法

k-core
定义
算法

degree(u)>degree(v):即看在order中在v(当前顶点)右边的v邻居
算法举例:page 34-50
k-truss
定义
算法

- 举例:page 54-63
k-clique
定义
原始算法

- 举例:page 69-79
算法KCLIST

- 举例:page 82-86(如果看不懂,建议先看简单算法的举例)
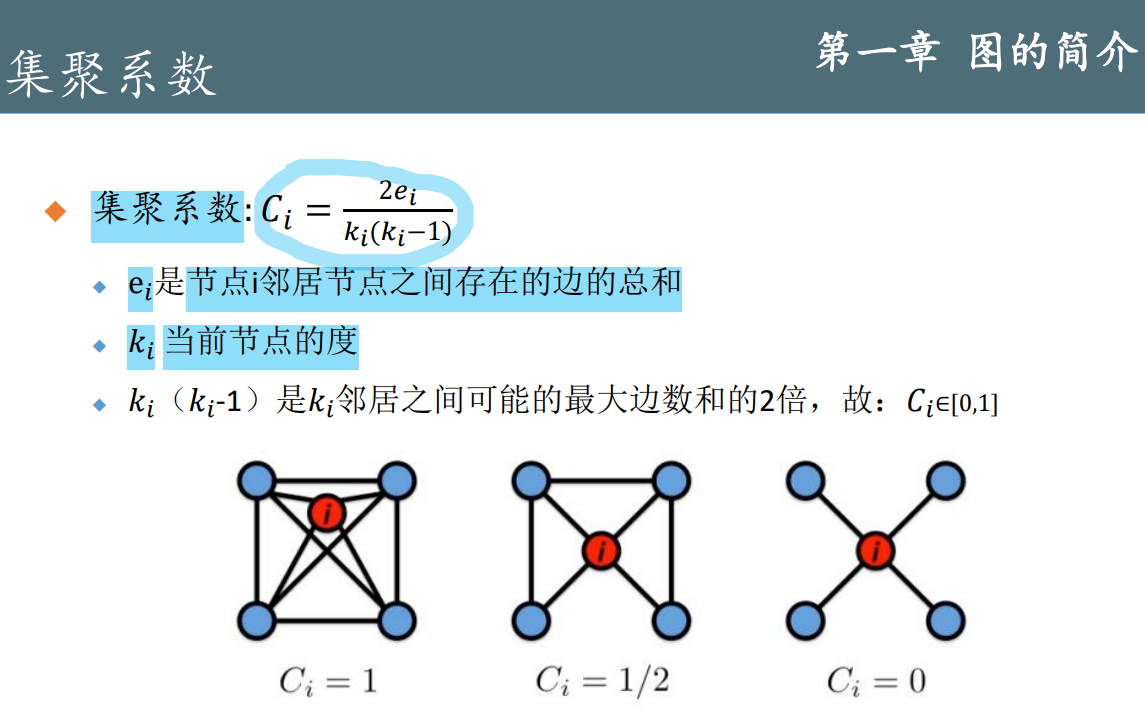
比较
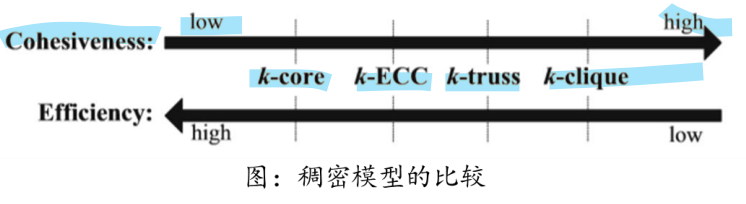
2.4 图关键字搜索
r-clique


分支限界算法


- 举例:page 20-33
k-NK搜索
二跳标签索引

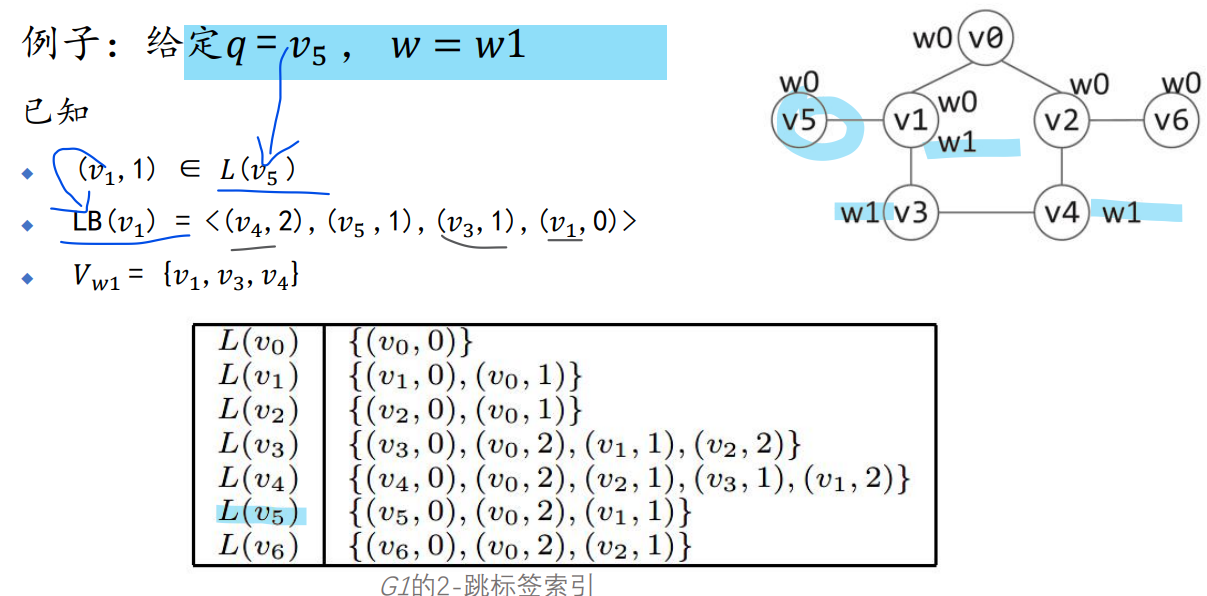
举例和应用:线性扫描L(v1)和L(v3)
k-Nk查询定义

前向搜索(FS)

其中“查找dist(q,vi)”通过查二跳标签索引L(q)和L(vi)得到
二跳标签后向索引
根据二跳标签索引L构建LB:

前向后向搜索(FBS)

举例:
2.5 图结构差异性搜索
基于连通分量的结构差异性
是一个顶点的性质

基于核心的结构差异性
是一个顶点的性质

问题 CC-TopK Core-TopK
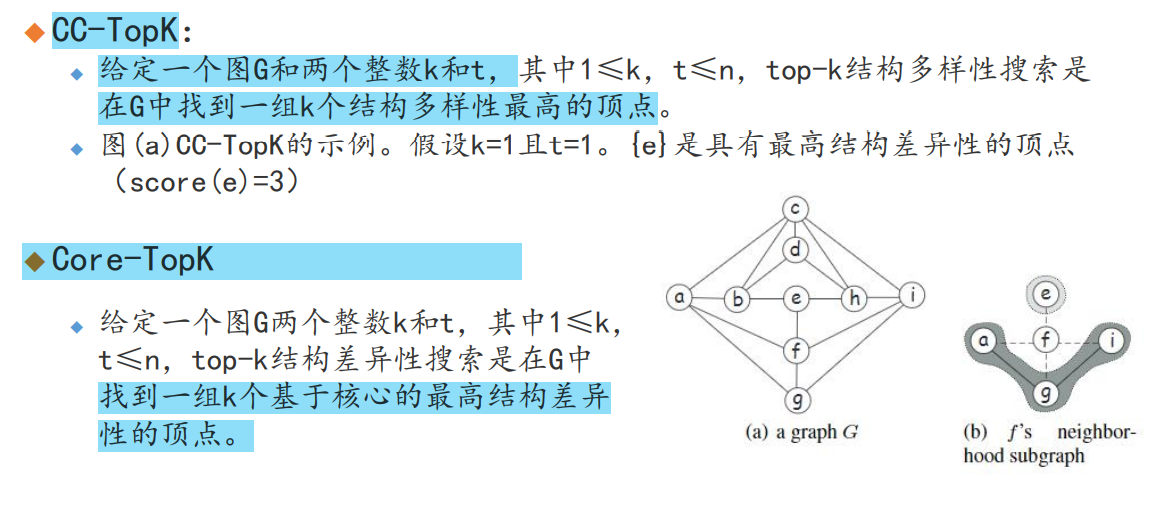
CC-TopK的基于度的简单方法
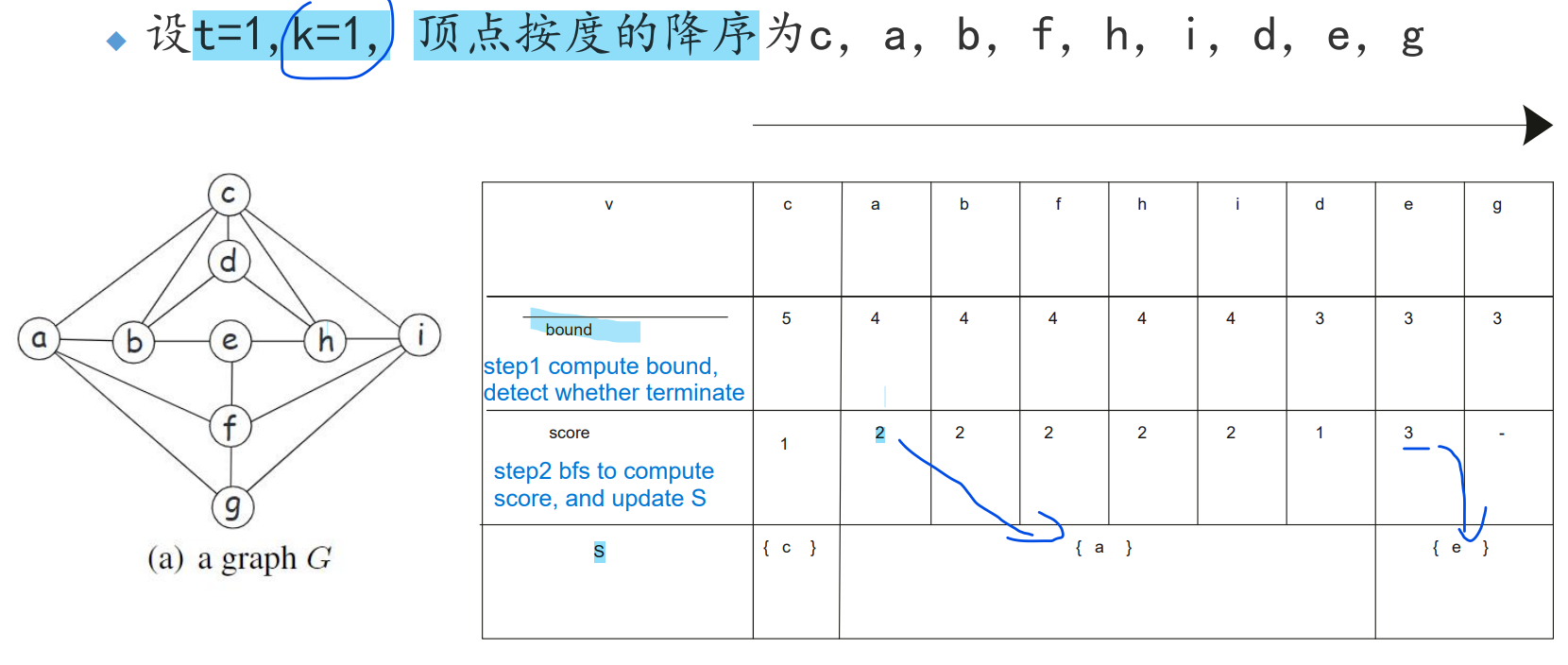
bound

算法


举例:
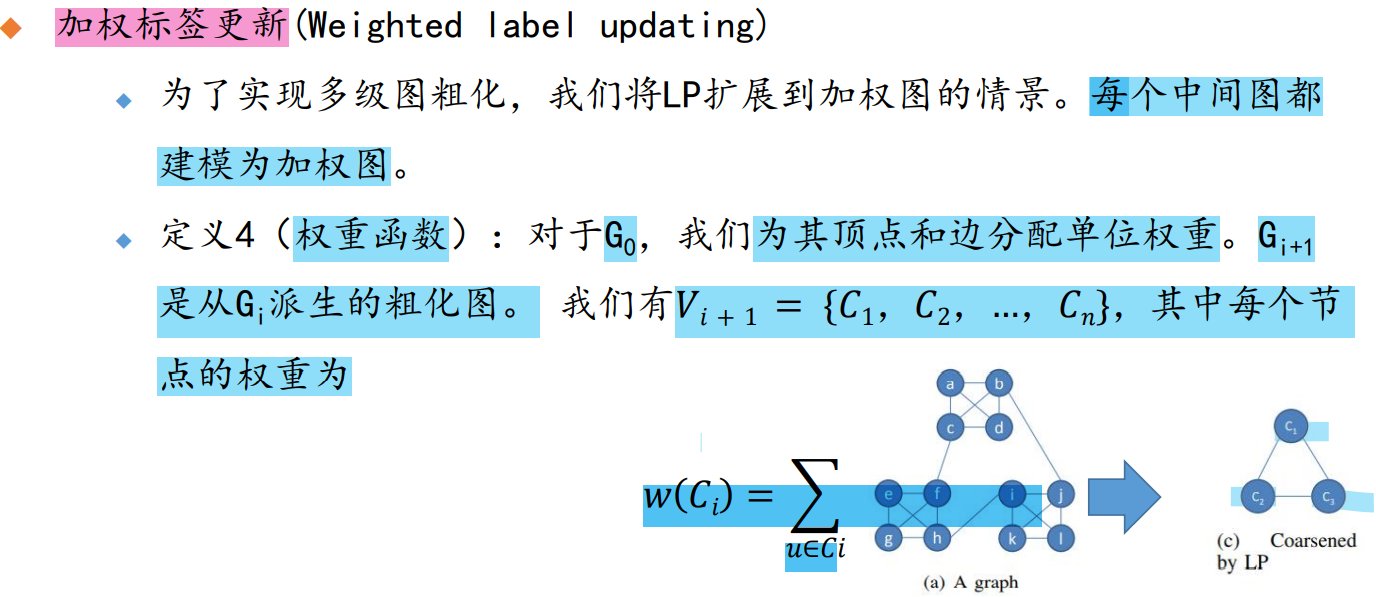
2.6 图划分
标签更新过程:

两个扩展:(当多个标签具有相同的最高频率,不再是随机选一个)

定义:

3.1 社区检测 COPRA
重叠社区发现算法COPRA
算法
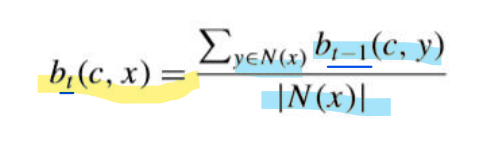


举例
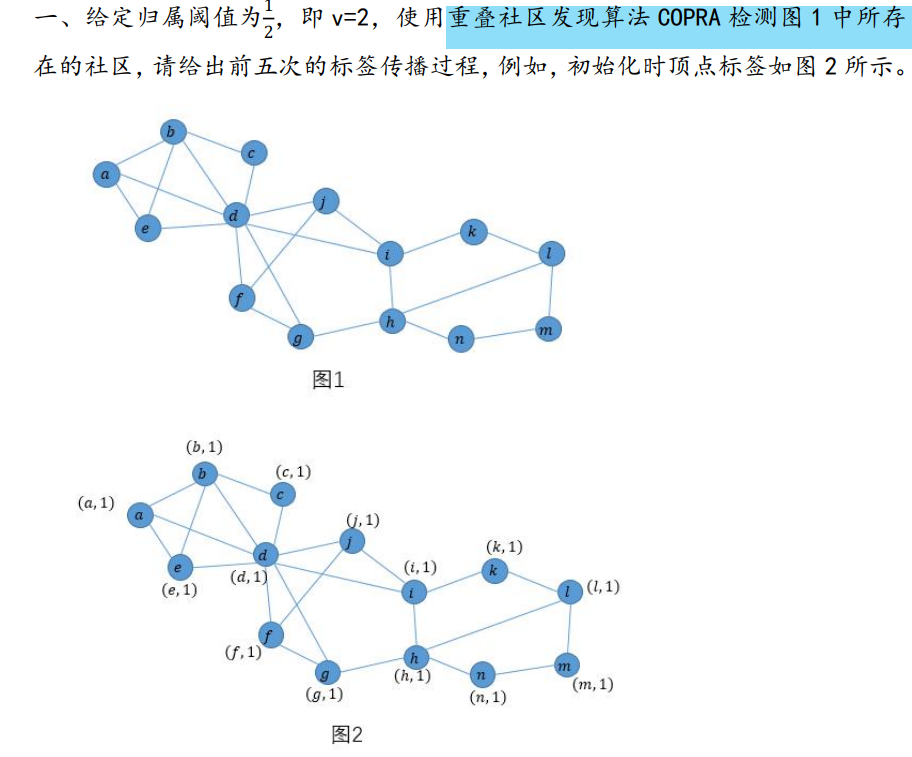
解:
对于每个顶点:
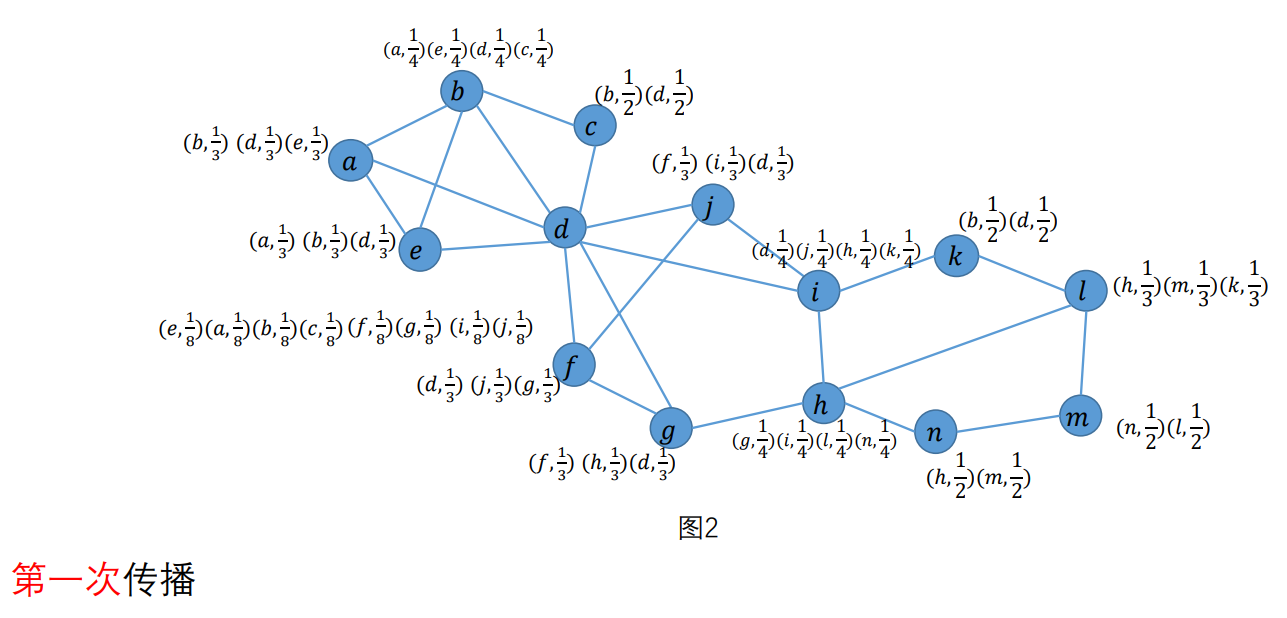
- 删除标签:系数>=1/2的标签保留;若所有标签都系数<1/2,则保留其中系数最高的标签;若有多个系数相同的这种标签,则随机保留其中一个;
- 对于保留的标签,进行系数归一化(所有标签系数之和为1)
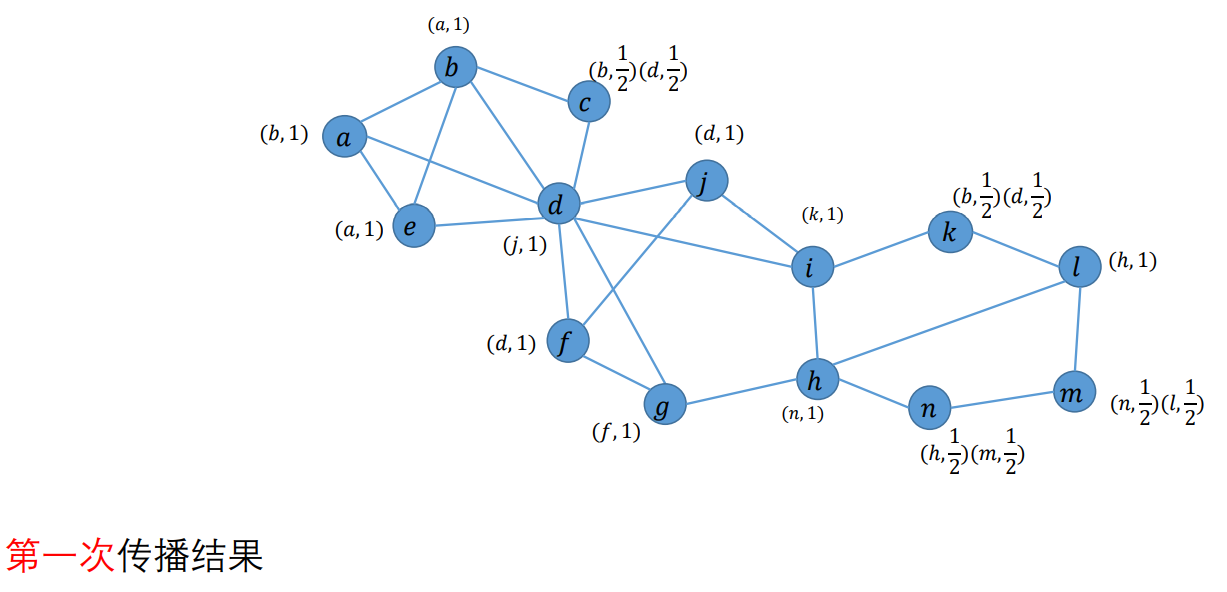
传播:对于每个顶点,对于其邻居中的每个标签L,扫描它的所有邻居将该标签的系数求和,再除以邻居数目,得到L的系数
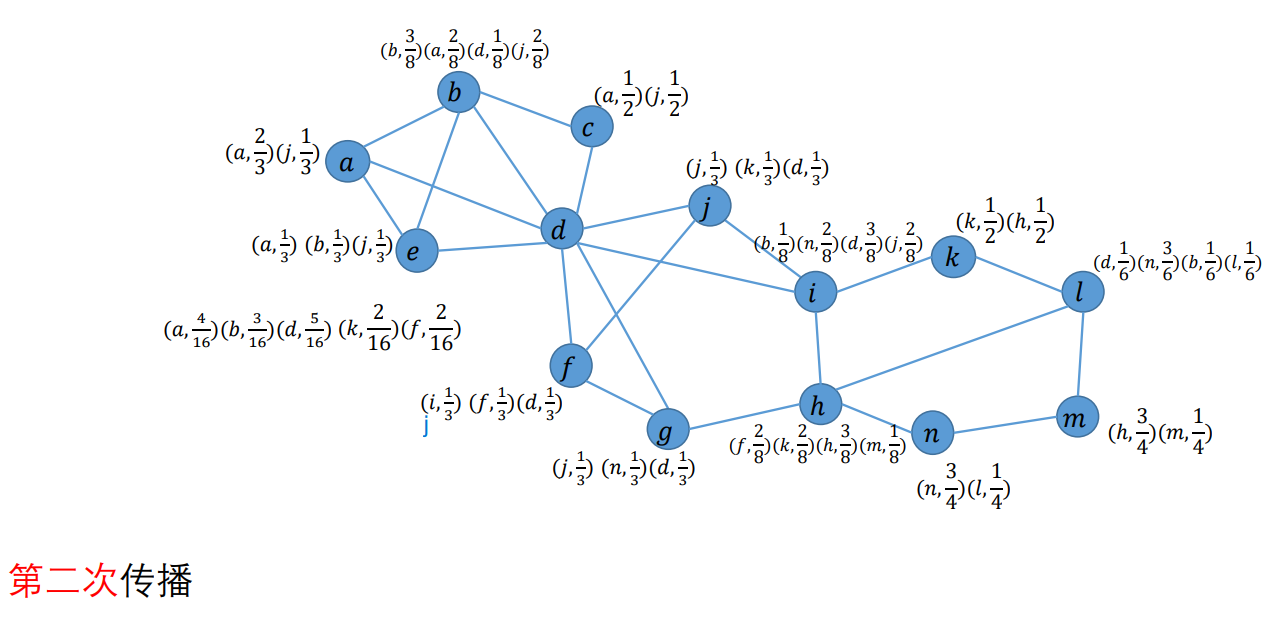
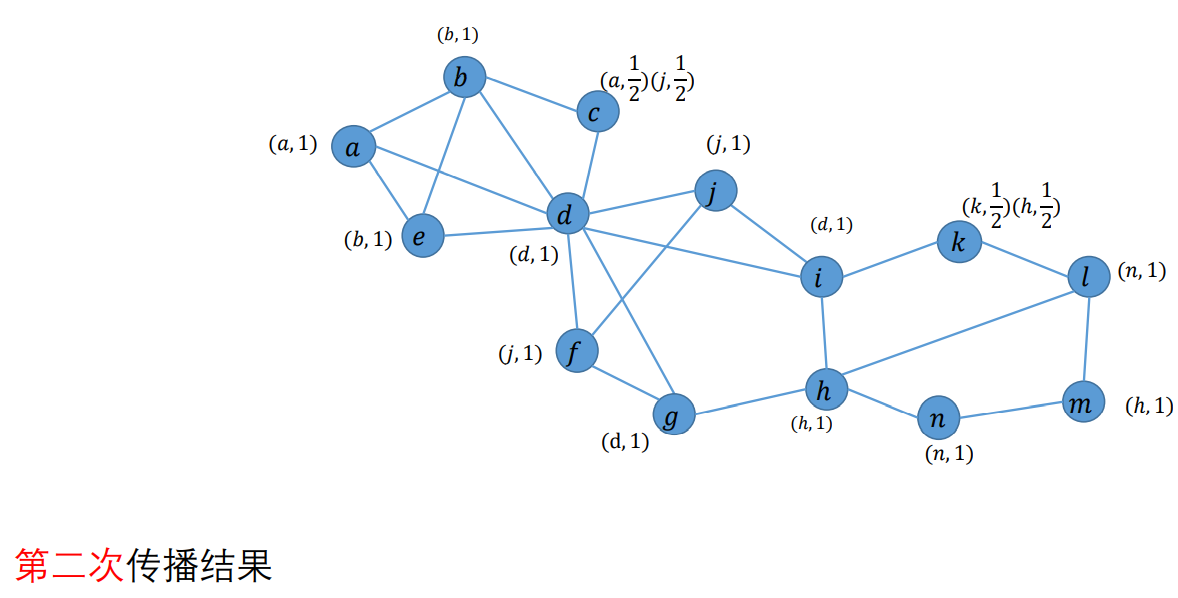
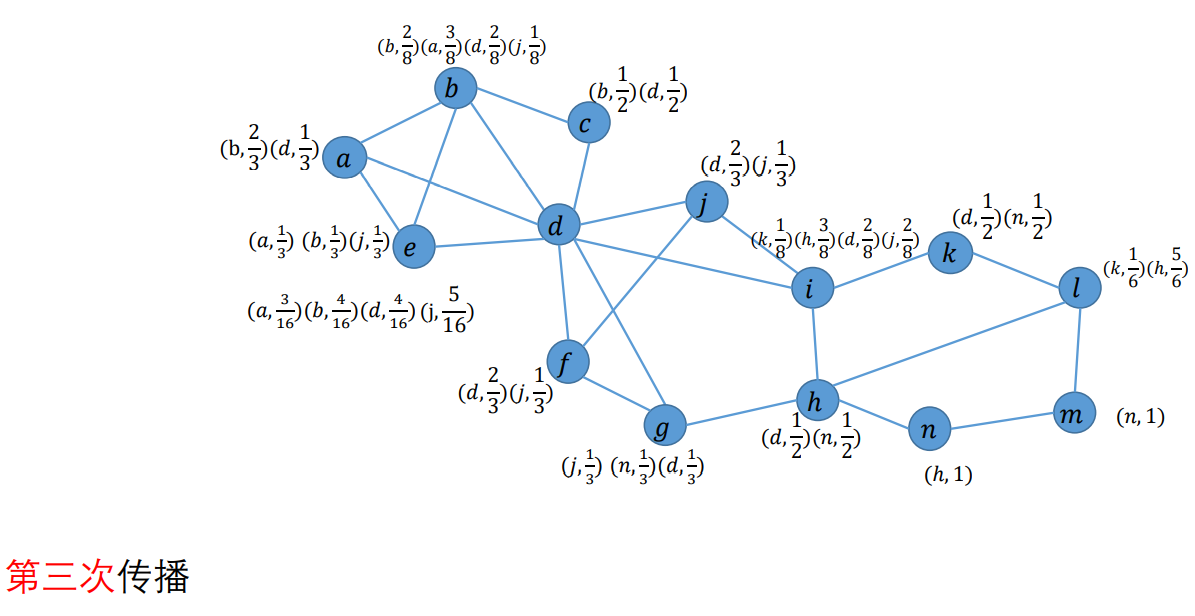
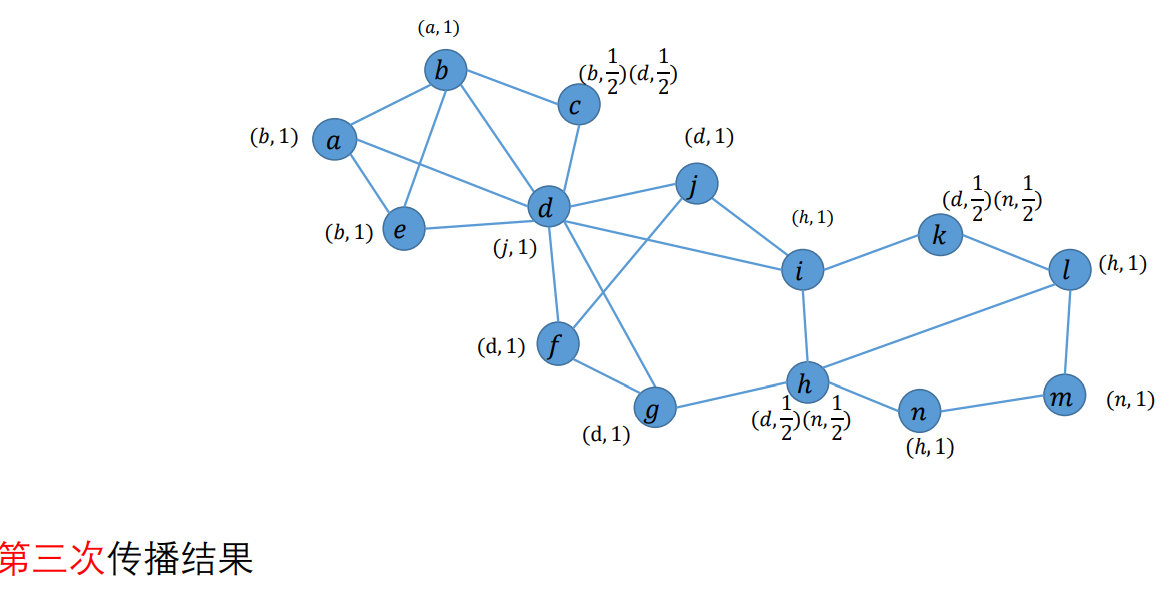
以此类推,见作业答案
3.2 异常检测
评测指标
- 精确率P,召回率R
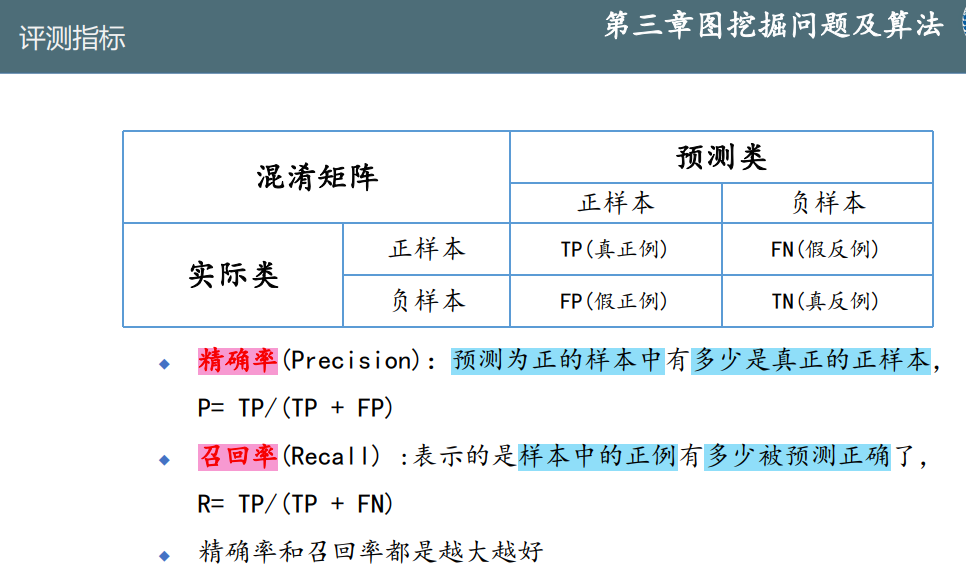
- F-measure(是P和R的一个平均数)

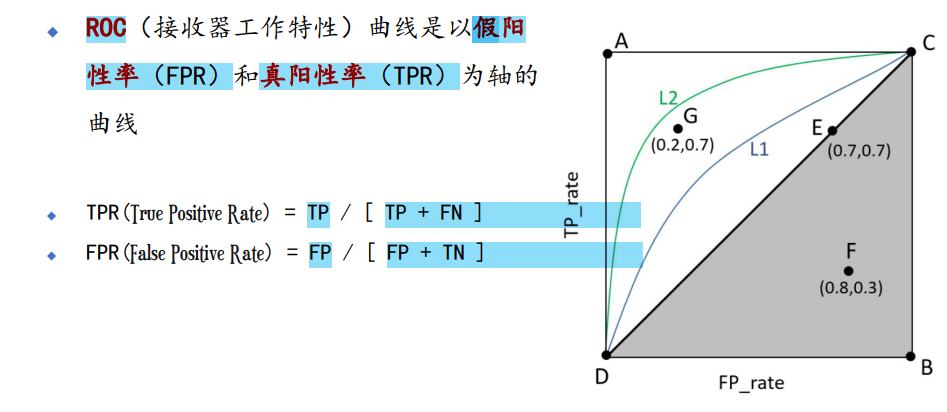
- ROC 曲线(TPR(即召回率):样本中的正例有多少被预测正确了;FPR:样本中的负例有多少被预测正确了)

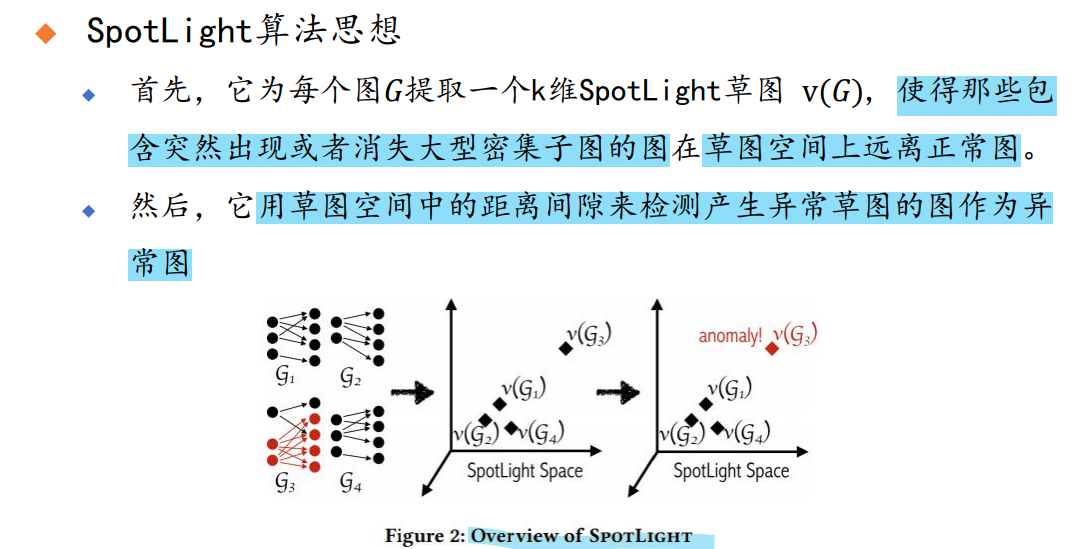
SpotLight 算法
图模型
每个Gt是一个有向二部图

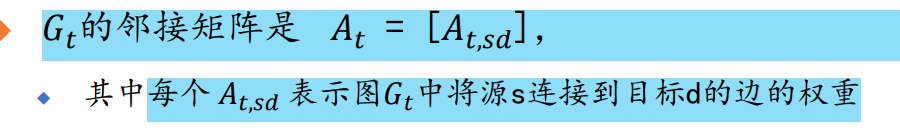

算法
- 如何提取spotlight草图v(G):先选取k个查询子图(分别对应v(G)坐标的k个维度),然后计算每个维度(对应查询子图的边权之和)

举例: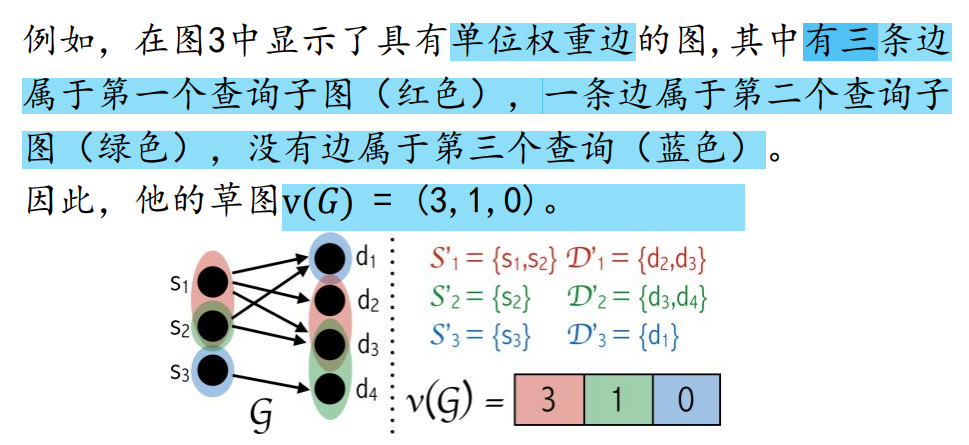
3.3 频繁子图挖掘
定义

子图的支持度:(在输入的多个图中的)出现次数
一个图中出现(不管多少次),计一次

举例:
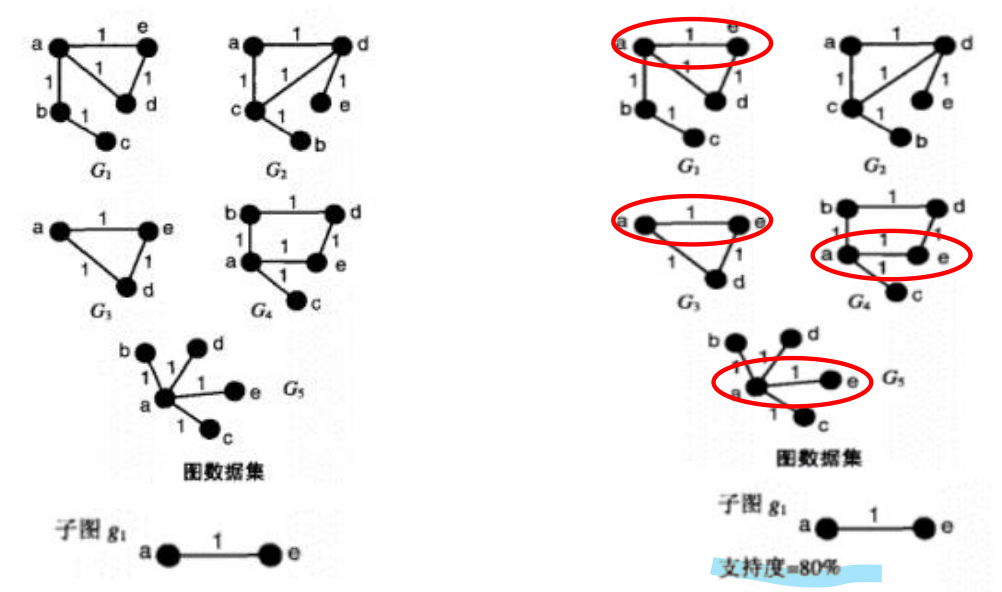
Apriori算法

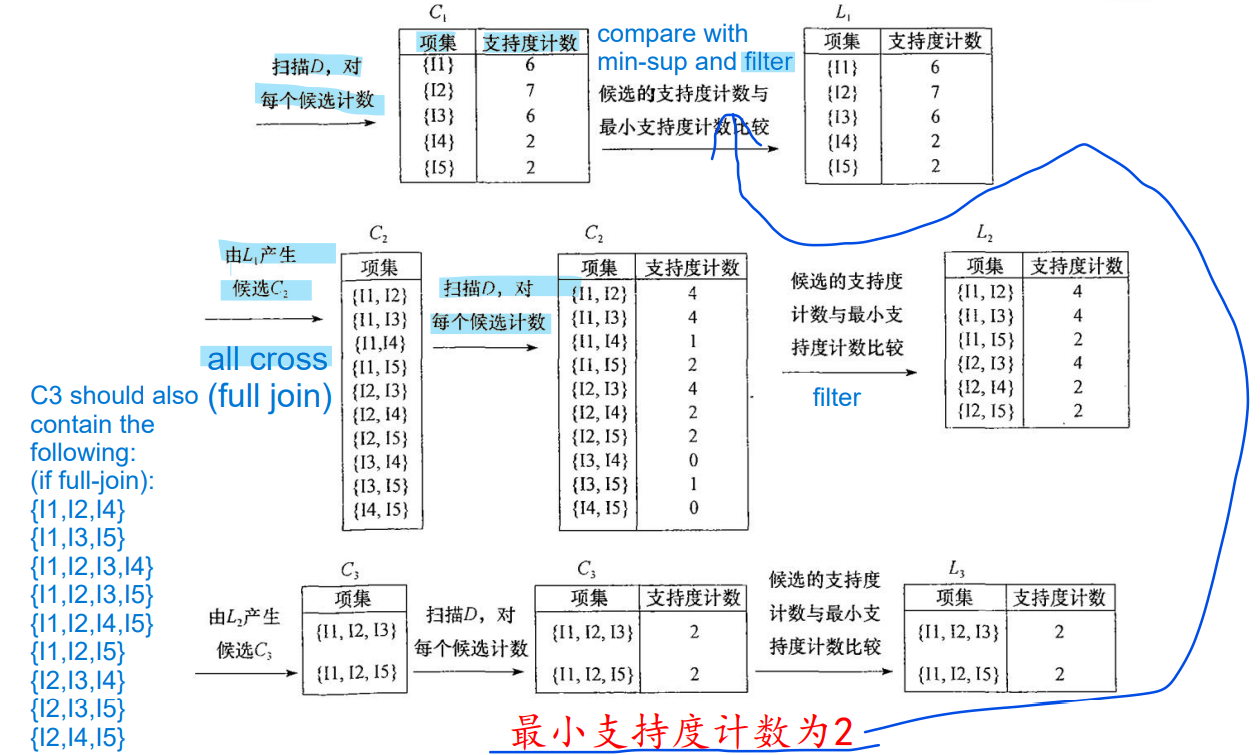
AGM 基于Apriori算法的频繁子图挖掘算法
图编码



合并两个含有k个顶点(且共有一个k-1个顶点的子图)的图:如果用编码

算法




3.5 图概要
无损图表示
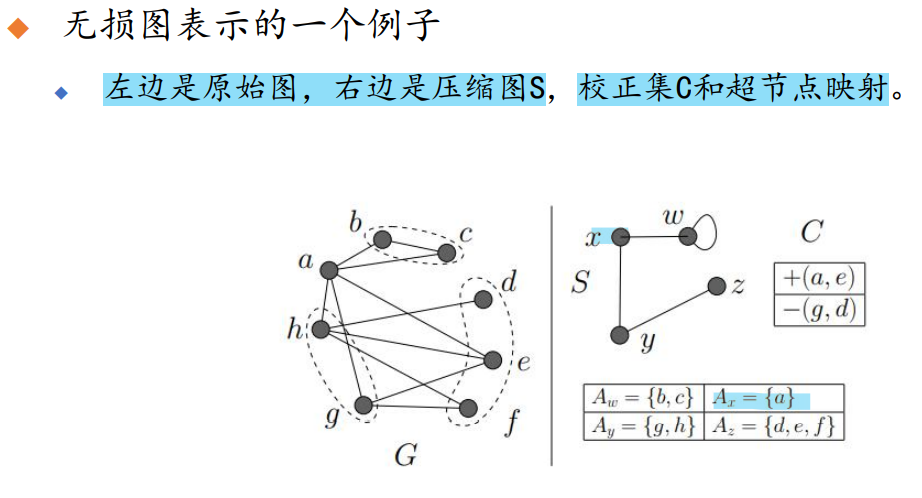
”超节点映射“:记录每个超节点代表原图中的哪些点
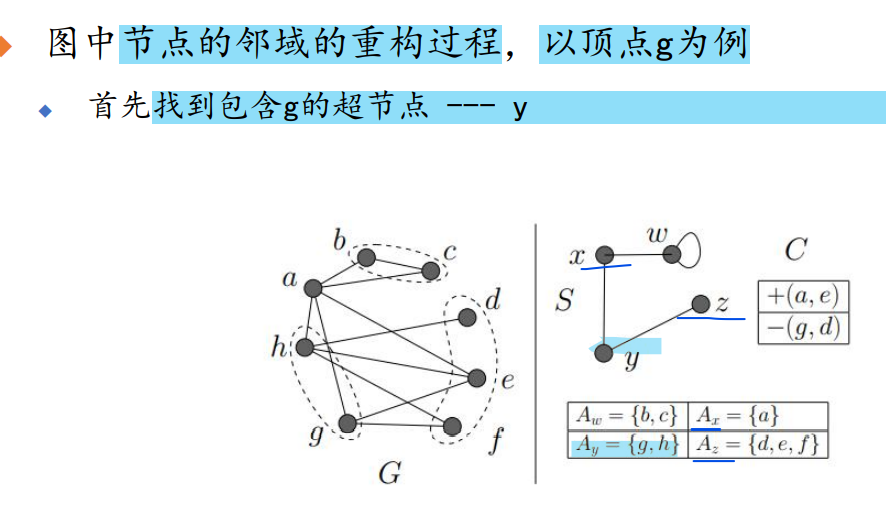

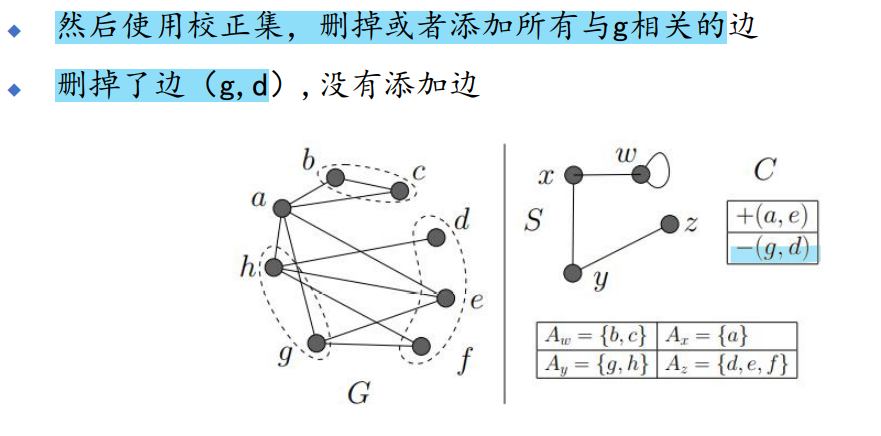

(超点连接的)存储开销



贪婪算法


算法




举例
s(x,y)计算举例 page42和page45
算法举例 page41-48