定义
bij:顶点Ni到顶点Nj间边Bij的容量
fij:顶点Ni到顶点Nj的最大流流量
F是fij构成的方阵
贡献
判定一个F是否能在某些网络拓扑中达到

判定算法:求fij;然后在构造最大生成树时检查是否违反这个
(1)可以自然推出:>=i-p任意“路径”(注意路径上“相邻”两点不需要有边相连)的minflow
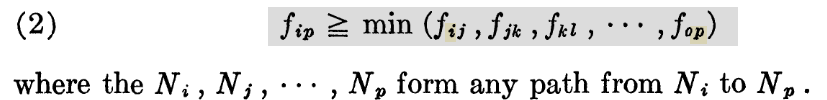
证明过程中提出:以fij作为边Bij的权重构造一棵最大生成树,对于任意一条不在该树上的边ip,i到p的最大流 等于 该树上i到p(唯一)的路径的minflow

condense graph
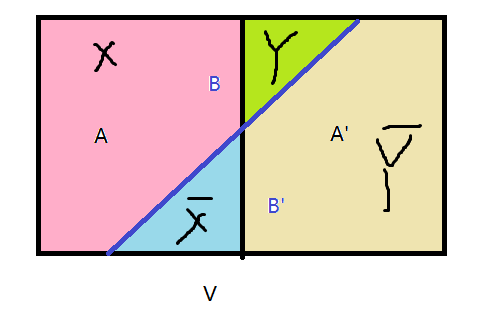
构造(注意(A,A’)是最小割)

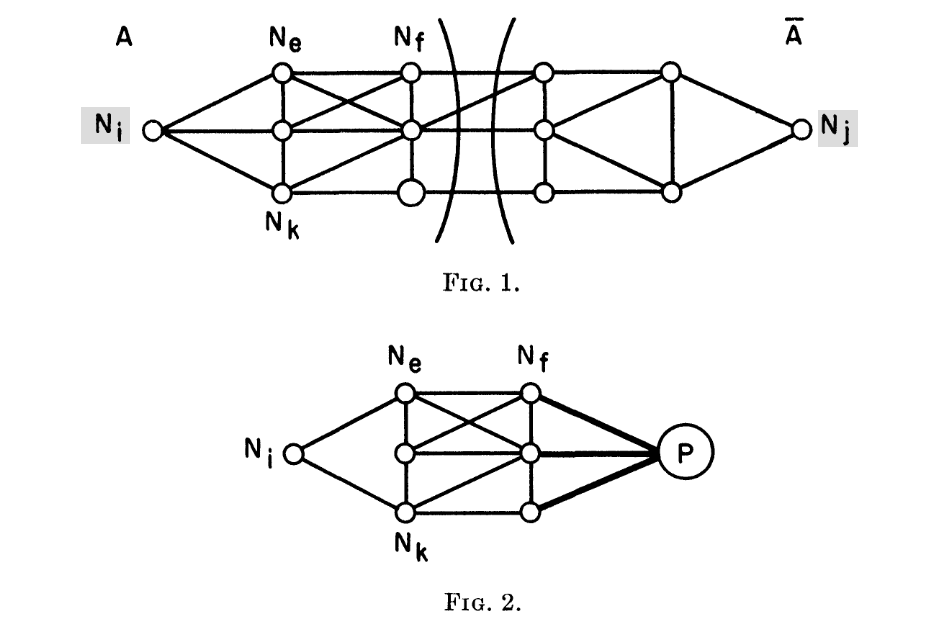
性质(ordinary nodes是指在A中(A中是因为A‘中的顶点在condense graph中已经被收缩成一个点了)、非Ni的顶点)
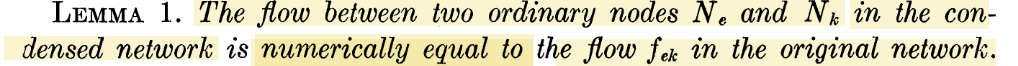
n-1次最大流求解就求出全图所有点对之间的最大流
不断做划分顶点的事,然后
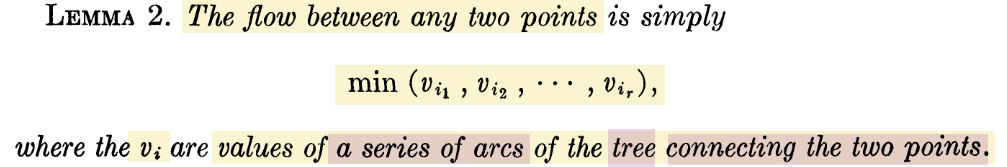
证明中提出的一个性质:

这个性质应用到最终划分所得树上,以及根据划分过程,得到最终树的性质:关键是这个性质使得可以n-1代替n(n-1)/2、进行合并:最终树的边既是cut又是maxflow,cut则两点间maxflow<=min(树上路径),maxflow则两点间maxflow>=min(树上路径),因此两点间maxflow==min(树上路径)
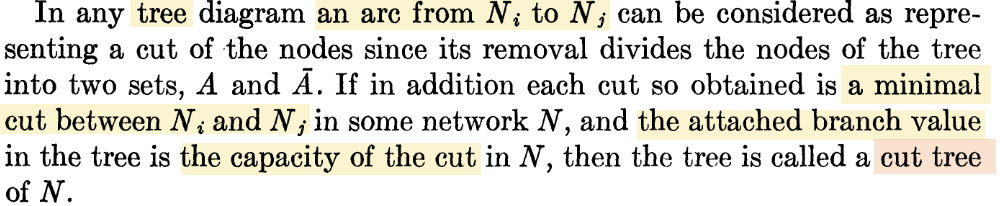
划分过程
原文描述完思路之后还有一个详细例子

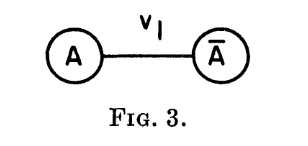


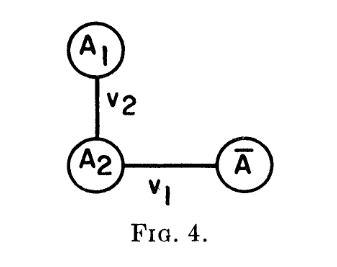

证明阅读
lemma1证明