defintions
- unit network单位网络:每个顶点要么只有一条出边且容量为1,要么只有一条入边且容量为1
- unit capacity network单位容量网络:所有边容量=1
reductions of problem version
undirected->directed
https://stackoverflow.com/questions/29741691/maximum-flow-in-the-undirected-graph
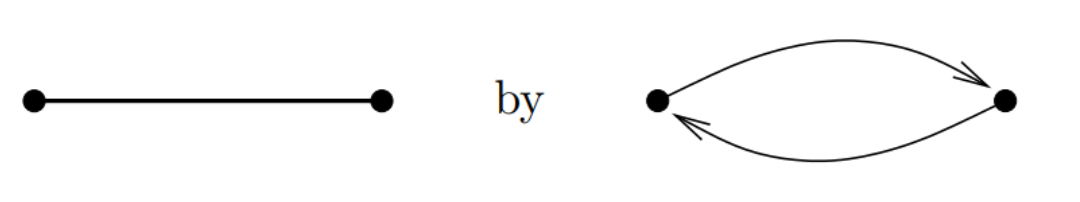
正确性:
- for max-flow:It can be easily proven that in such conversion, flow only propagates through one of the two edges and always one of them is not used
max flow: directed->undirected
Faster Energy Maximization for Faster Maximum Flow
方法:

证明:
directed vertex disjoint -> directed edge disjoint
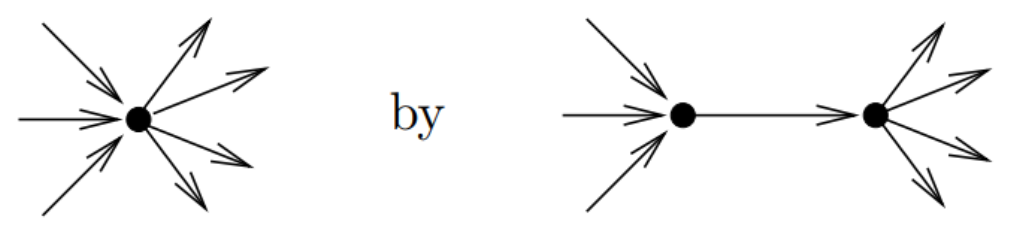
general relationship between max-flow and disjoint
edge-disjoint -> max-flow
对于单位容量、整数流的网络,augment paths after adjustment are edge-disjoint:edge-disjoint来自于 边容量都是1,流是{0,1}流
最大流最小割定理


这个定理可以看出,最大流的大小取决于网络拓扑(因为等于最小s-t割的容量)
定义
- augment path for f in G:s-t path in Gf
- Gf:残余网络,G上流上f得到的:对于流f流过的边(u,v),正向边(u,v)的容量为c(u,v)-f(u,v),反向边(v,u)的容量为f(u,v)
- s-t cut:顶点集的划分
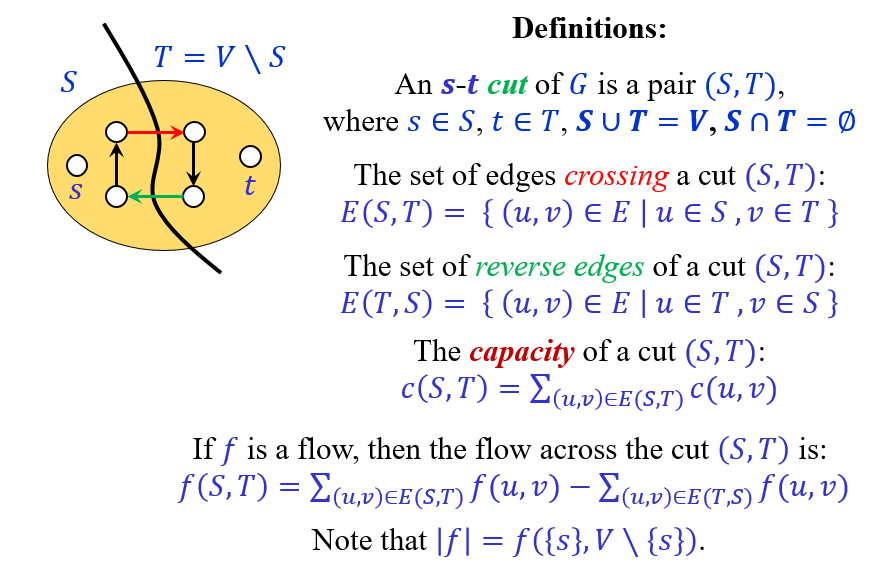
proof


因此证明只需要 在对f没有augment path时,找到一个s-t cut满足这个iff后面的特征即可,下面找这个s-t cut


if then是因为 没有augment path for f,则没有s-t path in Gf,所以Ef中一些边不存在
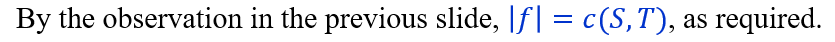
2 disjoint path
第一条augment path的选择,
正确性
定理的(2)->(1):对于f没有augment path -> f是G中最大流
因此 对于最大流>=2的单位容量、整数流网络,随意选择第一条augment path,都一定可以找到第二条augment path
因为 如果选择某条augment path作为第一条之后找不到其他augment path了,则根据“对于f没有augment path -> f是G中最大流”有此时的flow就是最大流,但此时的流量只有1,这与流最大>=2矛盾,所以一定可以找到第二条augment path
(2)->(1) proof框架(详细见下方proof):如果对f不存在augment path,则存在s-t cut满足c(S,T)=|f|(注意这个是全局的而不是局部的!),则f是最大流
效率(时间复杂度)
随意选择第一条augment path都一定可以找到第二条augment path的话,则考虑怎样选取进行求解的速度最快
如何选取第一条和第二条augment path,使得效率最高?



