思考
目前没有看完,刚看完central path的定义,在看norm的定义,浏览了下算法overall,似乎文章主要目标在max-flow的max,augment path的步骤文章中是直接说执行这个步骤,即这个步骤和往昔的max-flow算法是一样的,而++max-flow的disjoint是cancel flow提供的++,通过augment path步骤构造路径,而我们只需要两条augment path即可,这样似乎没有必要阅读全文:
是否值得继续阅读取决于一个问题:即第一条augment path的选择是否会影响能否找到两条以及找到两条的效率:
- 如果存在两条edge-disjoint,则若利用
cancel flow,是否对于任意的第一条augment path,都可以找到第二条augment path(从而修正一下得到两条edge-disjoint)? - 如果是的话,是否 对于第一条aygment path的选择,其可以对于整体找两条augment path有效率提升?
解决的问题
最大流:其中BT*f=tX即(BT*f即得到一个n维向量,表示每个顶点的净流量(出-入))满足flow conservation,所有顶点除了st都入流=出流,即净流=0,s是出,t是入,且s出量=t入量

V是标量,V的梯度(下三角)是m维向量(V对于每条边求偏导)
无向图
Preliminaries定义
d-flow
即满足顶点净流量==dv

ab-flow
即满足flow conservation

energy和electrical d-flow

能量回忆物理:电功率i^2*r
electrical d-flow即满足顶点净流量==dv、minimize能量的
maximum flow problem

Laplacian of the graph G with resistances r
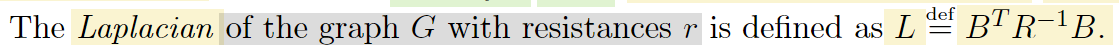
n*n矩阵,Lij=0,如果顶点ij之间没有边相连;=负的 ij间边电阻的倒数之和,如果顶点ij之间有边相连
B矩阵:对于每条边(即B的每行)只有两个端点(即B的每行只有两列非零,1和-1);B矩阵的每一列(即每个顶点的),表示对应顶点的出边入边情况
推导思考:
B转置*R-1得到的是:n*m矩阵,是B转置每一列都分别乘 该列对应的边的电阻的倒数
再乘以B,对于目标矩阵n*n的每个格子ij,思考:顶点i和j 的入边出边记录 对位相乘再相加 -> 对于每条边,这条边要么在顶点ij之间,要么不在,在的话对位相乘结果是”-1”(-1*1/r),不在的话则至少有一边是0,则对位相乘结果是0
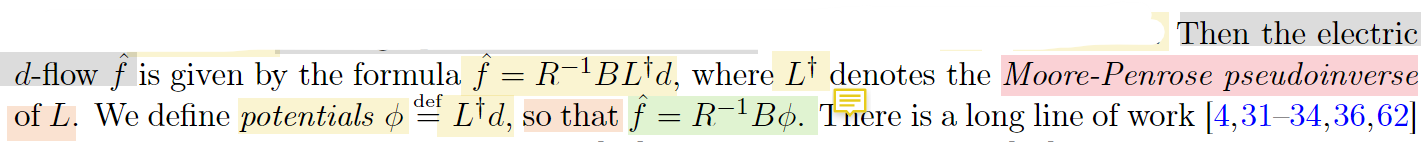
R-1*B,得到:m*n矩阵,是B矩阵每一行(每条边)都乘以对应边的电阻的倒数
可以看出求出φ就可以求出f帽
提出的定义
central path
为了转换优化问题,
观察到在最优时:
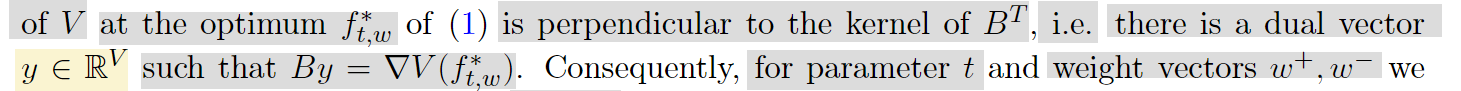
因此定义central path(满足V(f)最小时点(f,t,y)在central path上):
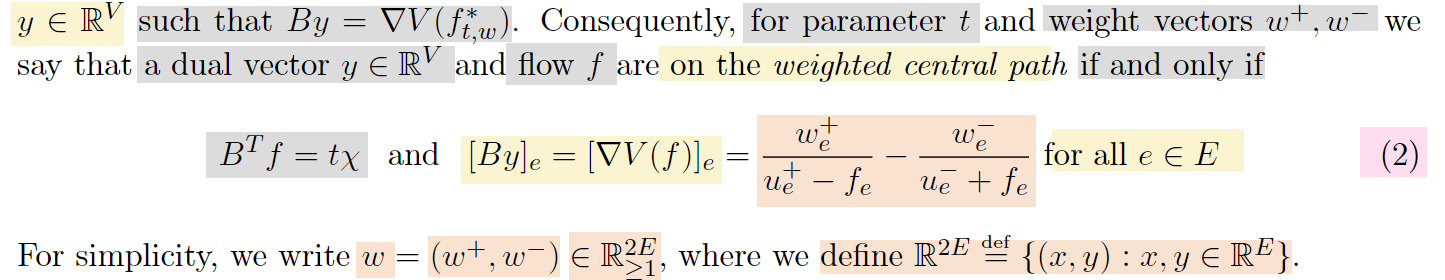
以及定义描述离central path距离的measurement:
- 先定义电阻
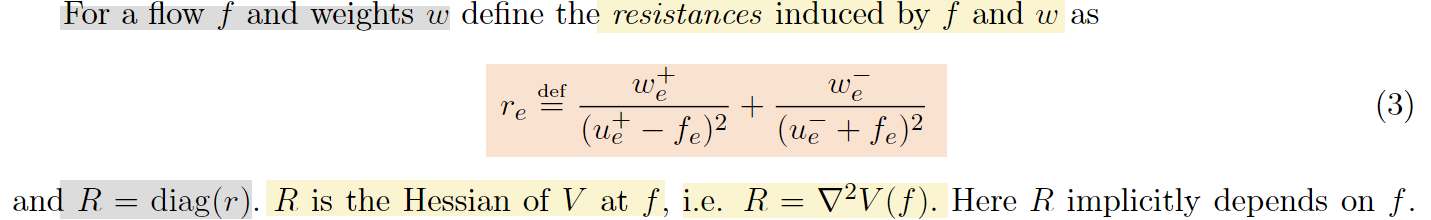
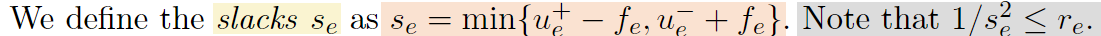
- 再定义measurement:

- 先定义电阻
也定义描述最大流距离“流最大”的measurement:
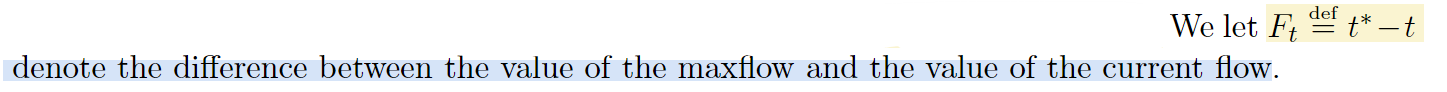
算法
overall





