红黑树本质上是一棵近似平衡的二叉查找树
红黑树的查找、插入、删除的时间复杂度最坏为O(log n)
回顾:二叉查找树
- 若任意结点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若任意结点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 任意结点的左、右子树也分别为二叉查找树。
- 没有键值相等的结点(no duplicate nodes)。
红黑树性质
红黑树的5条性质:
- 每个结点要么是红的,要么是黑的。
- 根结点是黑的。
- 每个叶结点(叶结点即指树尾端NIL指针)是黑的。
- 如果一个结点是红的,那么它的俩个儿子都是黑的。
- 对于任一结点而言,其到叶结点的每一条路径都包含相同数目的黑结点。
正是红黑树的这5条性质,使得一棵n个结点是红黑树始终保持了logn的高度
旋转
通过对结点进行重新着色,以及对树进行相关的旋转操作,即修改树中某些结点的颜色及指针结构,来达到对红黑树进行插入或删除结点等操作后,继续保持它的性质或平衡。
左旋
在某个结点x上做左旋操作:以x到y(x的右孩子)之间的链为“支轴”进行,它使y成为该孩子树新的根,y的左孩子b成为x的右孩子
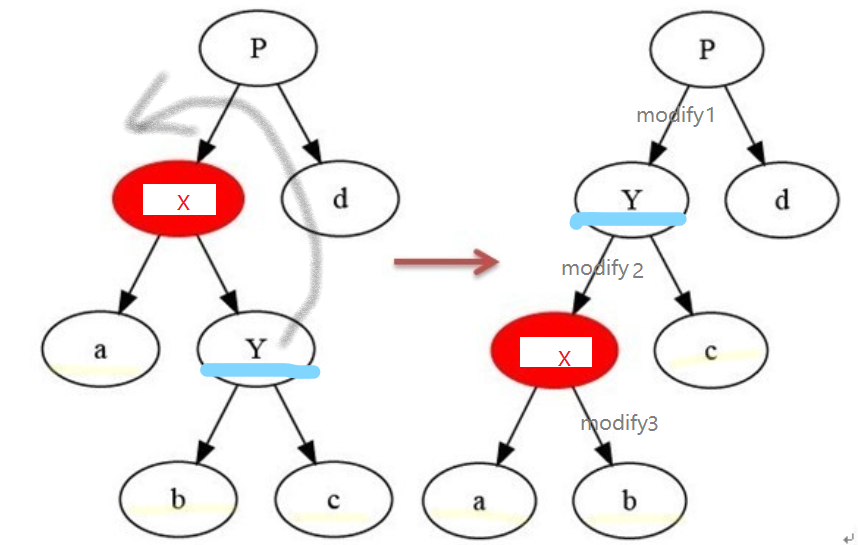
#p[v]是v的父亲,left[v]right[v]是v的左右孩子
def LEFT-ROTATE(T, x): #在x上做左旋
y ← right[x]
#modify3
right[x] ← left[y]
p[left[y]] ← x
#modify1
p[y] ← p[x]
if p[x] = nil[T] #x是根
then root[T] ← y
else if x = left[p[x]] #x是其父亲的左孩子
then left[p[x]] ← y
else right[p[x]] ← y #x是其父亲的右孩子
#modify2
left[y] ← x
p[x] ← y
右旋
在某个结点x上做右旋操作:以x到y(x的左孩子)之间的链为“支轴”进行,它使y成为该孩子树新的根,y的右孩子c成为x的左孩子
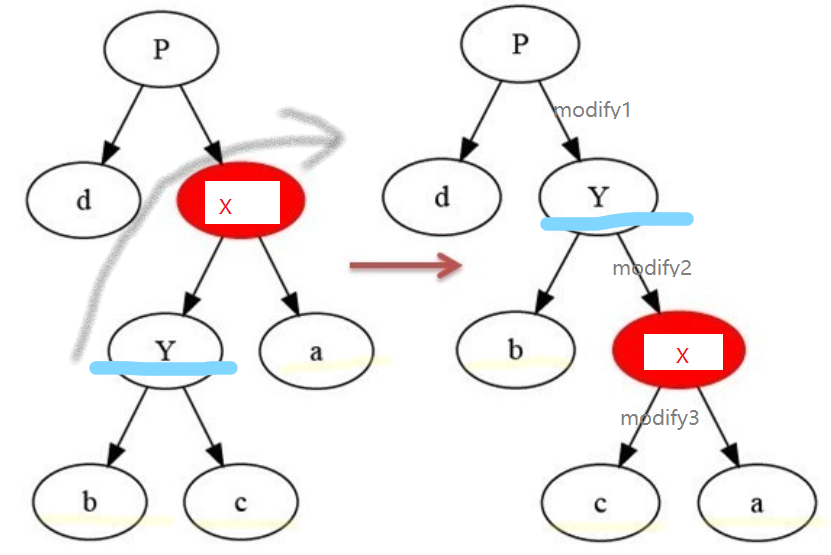
红黑树的插入
红黑树的插入相当于在二叉查找树插入的基础上,为了重新恢复平衡,继续做了插入修复操作。
向红黑树T中插入z:
- 搜索二叉树插入z
- 把z的左孩子、右孩子都赋为叶结点nil,再把z结点着为红色
- 旋转和调整着色
RB-INSERT(T, z)
# 搜索二叉树插入
1 y ← nil[T]
2 x ← root[T]
3 while x ≠ nil[T]
4 do y ← x
5 if key[z] < key[x]
6 then x ← left[x]
7 else x ← right[x]
8 p[z] ← y
9 if y = nil[T]
10 then root[T] ← z
11 else if key[z] < key[y]
12 then left[y] ← z
13 else right[y] ← z
# 涂色
# 把z的左孩子、右孩子都赋为叶结点nil,再把z结点着为红色
14 left[z] ← nil[T]
15 right[z] ← nil[T]
16 color[z] ← RED
# 旋转和调整着色
17 RB-INSERT-FIXUP(T, z)
旋转和调整着色
RB-INSERT-FIXUP(T,z) 1 while color[p[z]] = RED 2 do if p[z] = left[p[p[z]]] 3 then y ← right[p[p[z]]] 4 if color[y] = RED 5 then color[p[z]] ← BLACK 6 color[y] ← BLACK 7 color[p[p[z]]] ← RED 8 z ← p[p[z]] 9 else if z = right[p[z]] 10 then z ← p[z] 11 LEFT-ROTATE(T, z) 12 color[p[z]] ← BLACK 13 color[p[p[z]]] ← RED 14 RIGHT-ROTATE(T, p[p[z]]) 15 else (same as then clause with "right" and "left" exchanged) 16 color[root[T]] ← BLACK
while当前节点的父结点着色还是红色的,就继续调整
1 while color[p[z]] = RED
此时父结点的父结点一定存在,因为如果没有父结点即是根,而根不能是红色的
插入修复情况1:当前结点的父结点是红色且祖父结点的另一个子结点(叔叔结点)是红色
即如下代码所示:
2 do if p[z] = left[p[p[z]]] # 如果父亲是祖父的左孩子
3 then y ← right[p[p[z]]]
4 if color[y] = RED
将当前结点的父结点和叔叔结点涂黑,祖父结点涂红,从祖父结点重新开始算法
5 then color[p[z]] ← BLACK
6 color[y] ← BLACK
7 color[p[p[z]]] ← RED
8 z ← p[p[z]]
当前一定是红色




